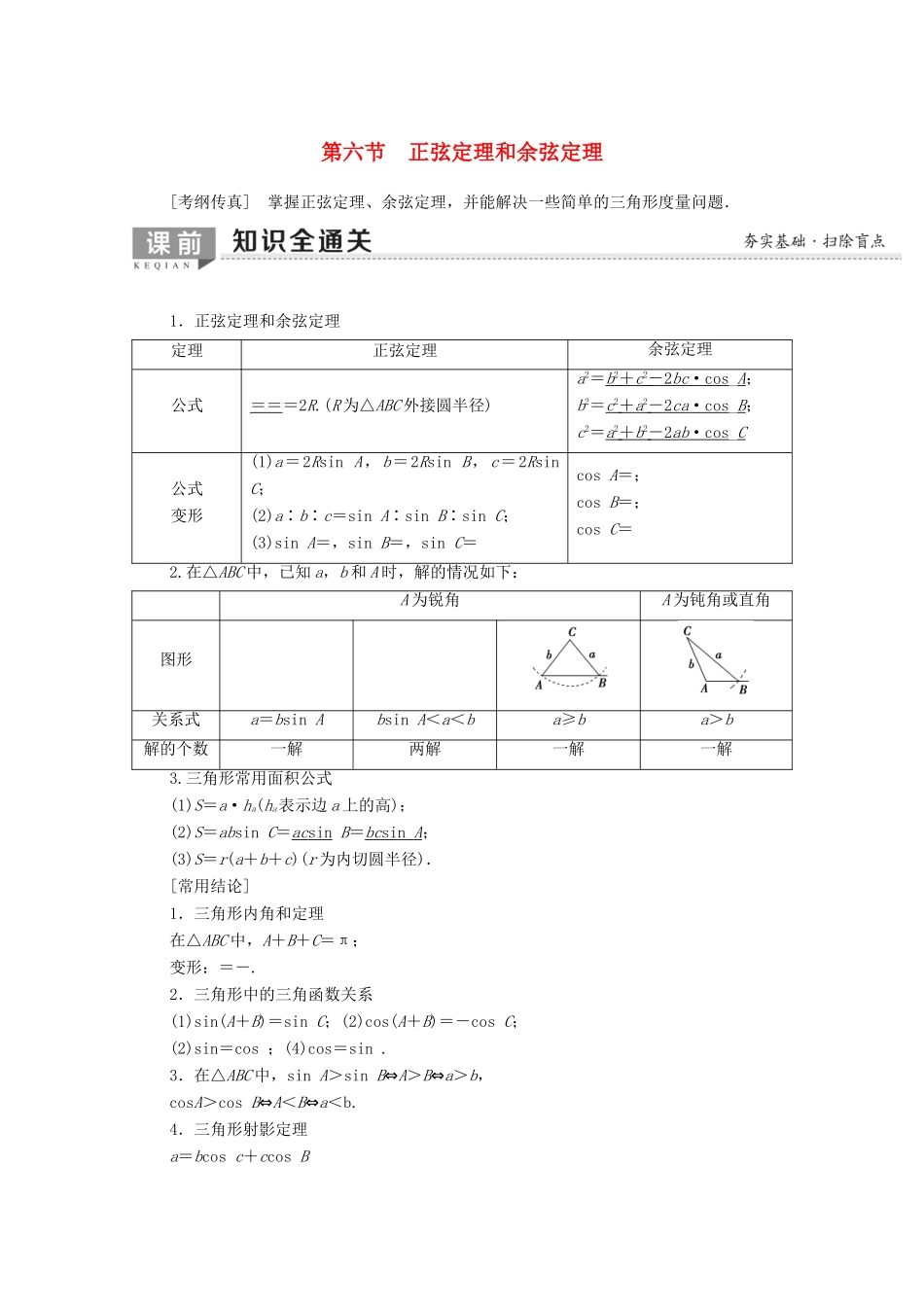
第六节 正弦定理和余弦定理[考纲传真] 掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.1.正弦定理和余弦定理定理正弦定理余弦定理公式===2R.(R 为△ABC 外接圆半径)a2=b 2 + c 2 - 2 bc ·cos _A;b2=c 2 + a 2 - 2 ca ·cos _B;c2=a 2 + b 2 - 2 ab ·cos _C公式变形(1)a=2Rsin A,b=2Rsin B,c=2Rsin C;(2)a∶b∶c=sin A∶sin B∶sin C;(3)sin A=,sin B=,sin C=cos A=;cos B=;cos C=2.在△ABC 中,已知 a,b 和 A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式a=bsin Absin A<a<ba≥ba>b解的个数一解两解一解一解3.三角形常用面积公式(1)S=a·ha(ha表示边 a 上的高);(2)S=absin C=ac sin B=bc sin A ;(3)S=r(a+b+c)(r 为内切圆半径).[常用结论]1.三角形内角和定理在△ABC 中,A+B+C=π;变形:=-.2.三角形中的三角函数关系(1)sin(A+B)=sin C;(2)cos(A+B)=-cos C;(2)sin=cos ;(4)cos=sin .3.在△ABC 中,sin A>sin B⇔A>B⇔a>b,cosA>cos B⇔A<B⇔a<b.4.三角形射影定理a=bcos c+ccos Bb=acos C+ccos Ac=acos B+bcos A5.三角形中任意两边之和大于第三边,任意两边之差小于第三边.[基础自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)在△ABC 中,若 A>B,则必有 sin A>sin B.( )(2)在△ABC 中,若 b2+c2>a2,则△ABC 为锐角三角形.( )(3)在△ABC 中,若 A=60°,a=4,b=4,则 B=45°或 135°.( )(4)在△ABC 中,=.( )[解析] (1)正确.A>B⇔a>b⇔sin A>sin B.(2)错误.由 cos A=>0 知,A 为锐角,但△ABC 不一定是锐角三角形.(3)错误.由 b<a 知,B<A.(4)正确.利用 a=2Rsin A,b=2Rsin B,c=2Rsin C,可知结论正确.[答案] (1)√ (2)× (3)× (4)√2.(教材改编)在△ABC 中,若 sin2A+sin2B<sin2C,则△ABC 的形状是( )A.锐角三角形 B.直角三角形C.钝角三角形 D.不能确定C [由正弦定理,得=sin A,=sin B,=sin C,代入得到 a2+b2<c2,由余弦定理得cos C=<0,所以 C 为钝角,所以该三角形为钝角三角形.]3.△ABC 的内角 A,B,C 的对边分别为 a,b,c,已知 a=,c=2,cos A=,则 b=( )A. B. C.2 D.3D [由余弦定理得 5=b...