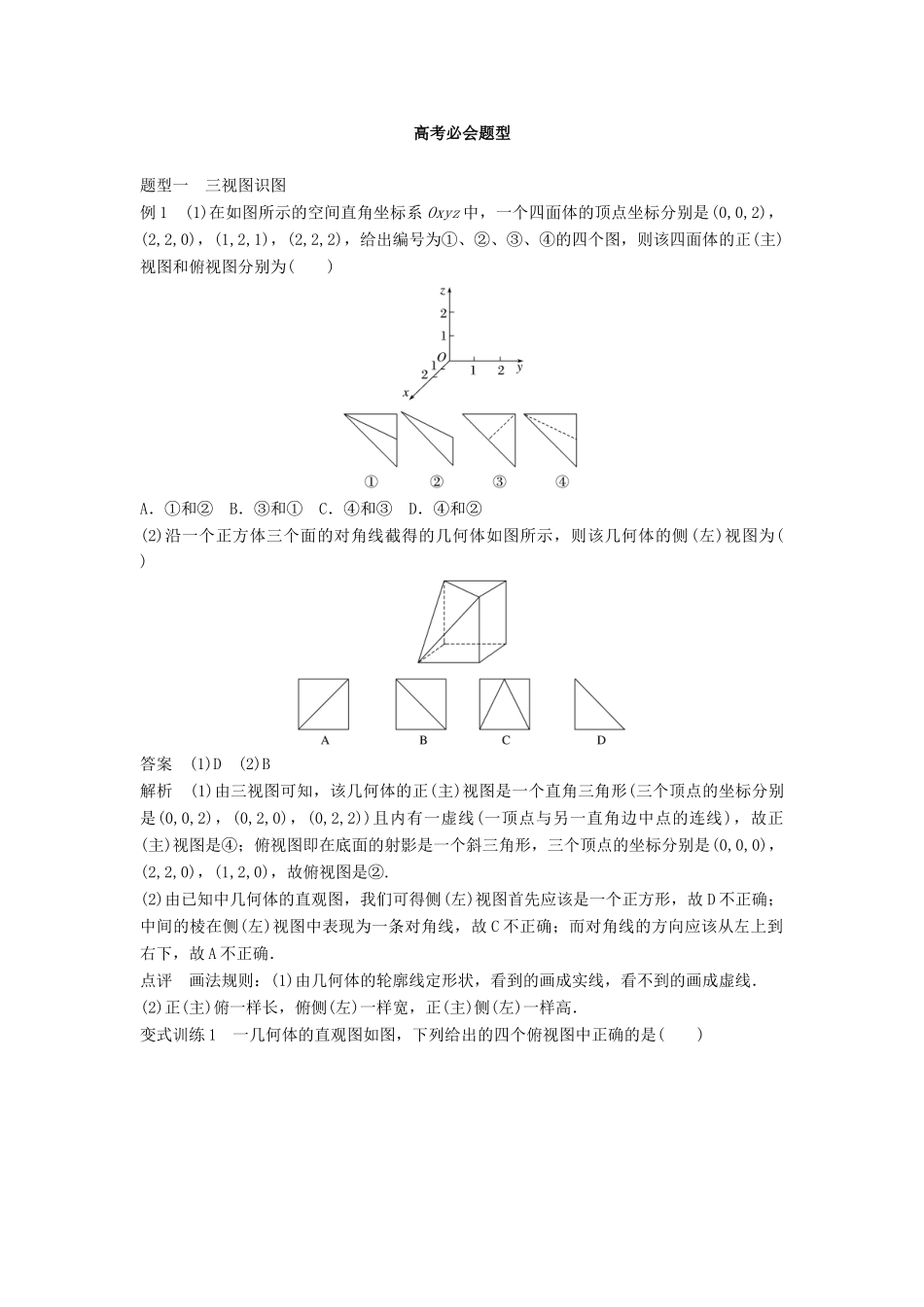
第25练空间几何体的三视图及表面积与体积[题型分析·高考展望]三视图是高考的热点和重点.其考查形式多种多样,选择题、填空题和综合解答题都有出现,而这些题目以选择题居多;立体几何中的计算问题考查的知识,涉及到三视图、空间几何体的表面积和体积以及综合解答和证明.体验高考1.(2015·陕西)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4答案D解析由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为S=2×π×12+×2π×1×2+2×2=π+2π+4=3π+4.2.(2016·课标全国乙)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π答案A解析由题意知,该几何体的直观图如图所示,它是一个球(被过球心O且互相垂直的三个平面)切掉左上角的后得到的组合体,其表面积是球面面积的和三个圆面积之和,由几何体的体积易得球的半径为2,则得S=×4π×22+3×π×22=17π,故选A.3.(2016·北京)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.1答案A解析由三视图知,三棱锥如图所示.由侧(左)视图得高h=1,又底面积S=×1×1=,所以体积V=Sh=.4.(2016·四川)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正(主)视图如图所示,则该三棱锥的体积是________.答案解析由题意可知,因为三棱锥每个面都是腰为2的等腰三角形,由正(主)视图可得俯视图(如图),且三棱锥高为h=1,则面积V=Sh=××1=.5.(2016·浙江)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是________cm2,体积是________cm3.答案8040解析由三视图可知该几何体由一个正方体和一个长方体组合而成,上面正方体的边长为2cm,下面长方体的底面边长为4cm,高为2cm,其直观图如图:其表面积S=6×22+2×42+4×2×4-2×22=80(cm2).体积V=2×2×2+4×4×2=40(cm3).高考必会题型题型一三视图识图例1(1)在如图所示的空间直角坐标系Oxyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号为①、②、③、④的四个图,则该四面体的正(主)视图和俯视图分别为()A.①和②B.③和①C.④和③D.④和②(2)沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的侧(左)视图为()答案(1)D(2)B解析(1)由三视图可知,该几何体的正(主)视图是一个直角三角形(三个顶点的坐标分别是(0,0,2),(0,2,0),(0,2,2))且内有一虚线(一顶点与另一直角边中点的连线),故正(主)视图是④;俯视图即在底面的射影是一个斜三角形,三个顶点的坐标分别是(0,0,0),(2,2,0),(1,2,0),故俯视图是②.(2)由已知中几何体的直观图,我们可得侧(左)视图首先应该是一个正方形,故D不正确;中间的棱在侧(左)视图中表现为一条对角线,故C不正确;而对角线的方向应该从左上到右下,故A不正确.点评画法规则:(1)由几何体的轮廓线定形状,看到的画成实线,看不到的画成虚线.(2)正(主)俯一样长,俯侧(左)一样宽,正(主)侧(左)一样高.变式训练1一几何体的直观图如图,下列给出的四个俯视图中正确的是()答案B解析该几何体是组合体,上面的几何体是一个五面体,下面是一个长方体,且五面体的一个面即为长方体的一个面,五面体最上面的棱的两端点在底面的射影距左右两边距离相等,因此选B.题型二空间几何体的表面积和体积例2(1)(2015·安徽)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.2+C.1+2D.2(2)(2015·天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.答案(1)B(2)π解析(1)由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S表=2××2×1+2××()2=2+,故选B.(2)由三视图可知,该几何体由相同底面的两圆锥和圆柱组成,底面半径为1m,圆锥的高为1m,圆柱的高为2m,所以该几何体的体积V=2×π×12×1+π×12×2=π(m3).点评利用三视图求几何体的表面积、体积,需先由三视图还原几何体,三个图形结合得出几何体的大致形状,由实、虚线得出局部位置的形状,再由...