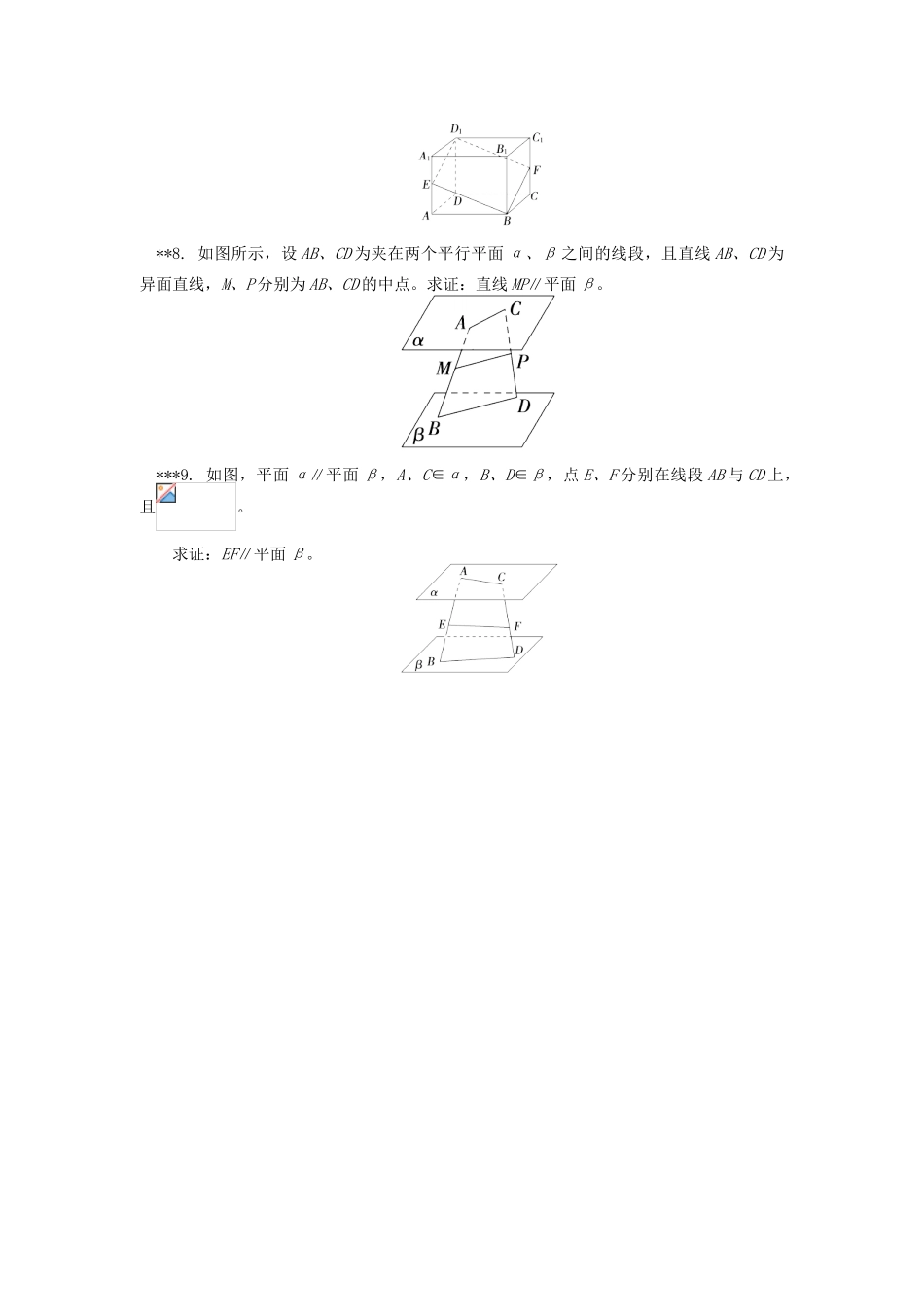
面面平行的性质(答题时间:40分钟)*1.若α∥β,且a⊂α,b⊂β,则直线a与b的位置关系是________。*2.若α∥β,a⊂α,下列三个说法中正确的是________。①a与β内所有直线平行;②a与β内的无数条直线平行;③a与β无公共点*3.若平面α∥平面β,且α、β间的距离为d,则在平面β内,下列说法正确的是________(填序号)。①有且只有一条直线与平面α的距离为d②所有直线与平面α的距离都等于d③有无数条直线与平面α的距离等于d④所有直线与平面α的距离都不等于d**4.(大连高一检测)在长方体ABCD-A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E、F,则四边形D1EBF的形状是________。**5.如图,P是△ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA、PB、PC于A′、B′、C′,若PA′∶AA′=2∶3,则=________。**6.如图,平面α∥平面β,△ABC与△A′B′C′分别在α、β内,线段AA′、BB′、CC′都交于点O,点O在α、β之间,若,OA∶OA′=3∶2,则△A′B′C′的面积为________。**7.如图所示,已知E、F分别是正方体ABCD-A1B1C1D1的棱AA1、CC1的中点,求证:四边形BED1F是平行四边形。**8.如图所示,设AB、CD为夹在两个平行平面α、β之间的线段,且直线AB、CD为异面直线,M、P分别为AB、CD的中点。求证:直线MP∥平面β。***9.如图,平面α∥平面β,A、C∈α,B、D∈β,点E、F分别在线段AB与CD上,且。求证:EF∥平面β。1.平行或异面解析:利用正方体模型可知a与b的位置关系可以平行,也可以异面。2.②③解析:a与平面β内的直线可能平行,也可能异面,但与β无公共点,故选②③。3.②③解析:由两平行平面间的距离可知,②③正确。4.平行四边形解析:如图,正方体ABCD-A1B1C1D1中,平面ABB1A1∥平面CDD1C1,过D1B的平面BED1F与平面ABB1A1交于直线BE,与平面CDD1C1交于直线D1F,由面面平行的性质定理,故BE∥D1F.同理BF∥D1E.所以四边形D1EBF为平行四边形。5.解析:由平面α∥平面ABC,得AB∥A′B′,BC∥B′C′,AC∥A′C′,由等角定理得∠ABC=∠A′B′C′,∠BCA=∠B′C′A′,∠CAB=∠C′A′B′,从而△ABC∽△A′B′C′,△PAB∽△PA′B′,==。6.解析:根据题意有,∵AA′、BB′相交,∴直线AA′、BB′确定一个平面ABA′B′,∵平面α∥平面β,∴AB∥A′B′,易得△ABO∽△A′B′O,①△ABC∽△A′B′C′,②由①得,由②得,∴。7.证明:取D1D的中点G,连接EG、GC,∵E是A1A的中点,G是D1D的中点,∴EG∥AD,由正方体性质知AD∥BC,∴EG∥BC,∴四边形EGCB是平行四边形,∴EB∥GC.①又∵G、F分别是D1D、C1C的中点,∴D1G∥FC,∴四边形D1GCF为平行四边形,∴D1F∥GC。②由①②得EB∥D1F。③∴E、B、F、D1四点共面,四边形BED1F是平面四边形,又∵平面ADD1A1∥平面BCC1B1,平面EBFD1∩平面ADD1A1=ED1,平面EBFD1∩平面BCC1B1=BF,∴ED1∥BF。④由③④得,四边形BED1F是平行四边形。8.证明:过点A作AE∥CD交平面β于E,连接DE、BE,∵AE∥CD,∴AE、CD确定一个平面,设为γ,则α∩γ=AC,β∩γ=DE。由于α∥β,∴AC∥DE(面面平行的性质定理)取AE中点N,连接NP、MN,∵M、P分别为AB、CD的中点,∴NP∥DE,MN∥BE。又NPβ,DEβ,MNβ,BEβ,∴NP∥β,MN∥β。又NP∩MN=N,∴平面MNP∥β。∵MP平面MNP,∴MP∥β。9.证明:(1)若直线AB和CD共面,∵α∥β,平面ABDC与α、β分别交于AC、BD两直线,∴AC∥BD。又∵,∴EF∥AC∥BD,∴EF∥平面β;(2)若AB与CD异面,连接BC并在BC上取一点G,使得,则在△BAC中,EG∥AC,AC平面α,∴EG∥α,又∵α∥β,∴EG∥β。同理可得:GF∥BD,而BDβ,∴GF∥β,∵EG∩GF=G,∴平面EGF∥β。又∵EF平面EGF,∴EF∥β。综合(1)(2)得EF∥β。