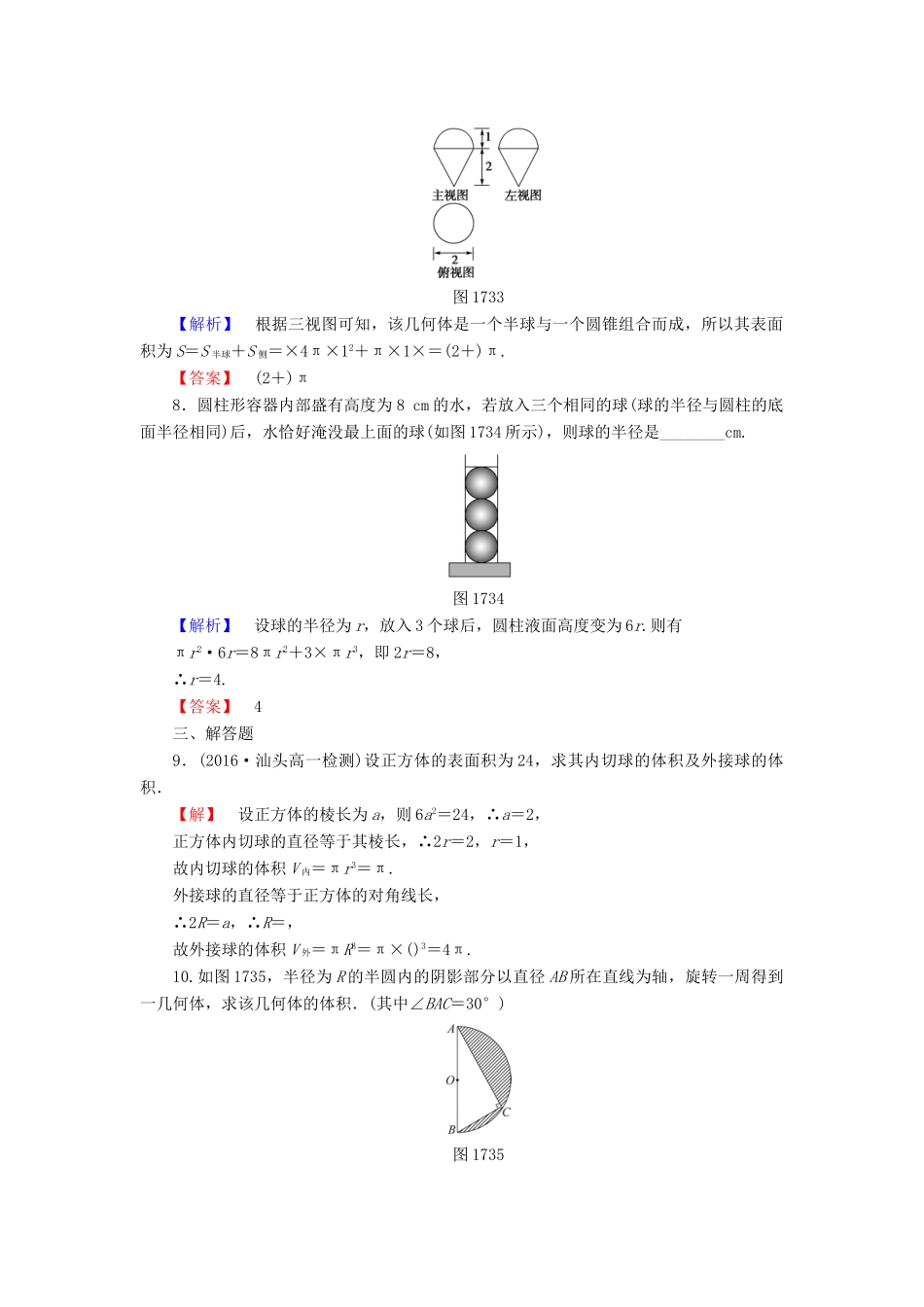
【课堂新坐标】2016-2017学年高中数学第一章立体几何初步学业分层测评12球北师大版必修2(建议用时:45分钟)[学业达标]一、选择题1.用与球心距离为1的平面去截球,所得截面面积为π,则球的体积为()A.πB.C.8πD.π【解析】设球的半径为R,截面的半径为r. πr2=π,∴r=1,∴R=,∴V=πR3=()3=π.【答案】D2.64个半径都为的球,记它们的体积之和为V甲,表面积之和为S甲;一个半径为a的球,记其体积为V乙,表面积为S乙,则()A.V甲>V乙且S甲>S乙B.V甲S乙D.V甲=V乙且S甲=S乙【解析】64个半径都为的球,它们的体积之和为V甲=64×π·=πa3,表面积之和为S甲=64×4π=16πa2;一个半径为a的球,其体积为V乙=πa3,表面积为S乙=4πa2,所以V甲=V乙且S甲>S乙,故选C.【答案】C3.一根细金属丝下端挂着一个半径为1cm的金属球,将它浸没在底面半径为2cm的圆柱形容器内的水中,现将金属丝向上提升,当金属球被拉出水面时,容器内的水面下降了()A.cmB.cmC.cmD.cm【解析】设容器内的水面下降了hcm,则球的体积等于水下降的体积,即π·13=π·22·h,解得h=.【答案】D4.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是,那么该三棱柱的体积是()【导学号:10690035】A.96B.16C.24D.48【解析】用平行于棱柱底面的平面去截棱柱和球,截面如图所示:设球的半径为R,则R3=,所以R=2.所以正三棱柱底面边长a=4,其高h=2R=4,V=×(4)2×4=48.【答案】D5.若与球相切的圆台的上、下底面半径分别为r,R,则球的表面积为()A.4π(r+R)2B.4πr2R2C.4πrRD.π(R+r)2【解析】法一:如图,设球的半径为r1,则在Rt△CDE中,DE=2r1,CE=R-r,DC=R+r.由勾股定理得4r=(R+r)2-(R-r)2,解得r1=.故球的表面积为S球=4πr=4πRr.法二:如图,设球心为O,球的半径为r1,连接OA,OB,则在Rt△AOB中,OF是斜边AB上的高.由相似三角形的性质得OF2=BF·AF=Rr,即r=Rr,故r1=,故球的表面积为S球=4πRr.【答案】C二、填空题6.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为________.【解析】如图所示,设球半径为R,底面中心为O′且球心为O, 正四棱锥PABCD中AB=2,∴AO′=. PO′=4,∴在Rt△AOO′中,AO2=AO′2+OO′2,∴R2=()2+(4-R)2,解得R=,∴该球的表面积为4πR2=4π×=.【答案】7.如图1733是一个几何体的三视图,则该几何体的表面积为________.图1733【解析】根据三视图可知,该几何体是一个半球与一个圆锥组合而成,所以其表面积为S=S半球+S侧=×4π×12+π×1×=(2+)π.【答案】(2+)π8.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图1734所示),则球的半径是________cm.图1734【解析】设球的半径为r,放入3个球后,圆柱液面高度变为6r.则有πr2·6r=8πr2+3×πr3,即2r=8,∴r=4.【答案】4三、解答题9.(2016·汕头高一检测)设正方体的表面积为24,求其内切球的体积及外接球的体积.【解】设正方体的棱长为a,则6a2=24,∴a=2,正方体内切球的直径等于其棱长,∴2r=2,r=1,故内切球的体积V内=πr3=π.外接球的直径等于正方体的对角线长,∴2R=a,∴R=,故外接球的体积V外=πR3=π×()3=4π.10.如图1735,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的体积.(其中∠BAC=30°)图1735【解】过C作CO1⊥AB于O1,在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,∴AC=R,BC=R,CO1=R.AO1=AC·sin60°=R,BO1=AB-AO1=,∴V球=πR3.V圆锥AO1=·π··R=πR3,V圆锥BO1=·π··R=πR3,V几何体=V球-V-V=πR3-πR3-πR3=πR3.[能力提升]1.如图1736,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的体积为()图1736A.cm3B.cm3C.cm3D.cm3【解析】如图,作出球的一个截面,则MC=8-6=2(cm)...