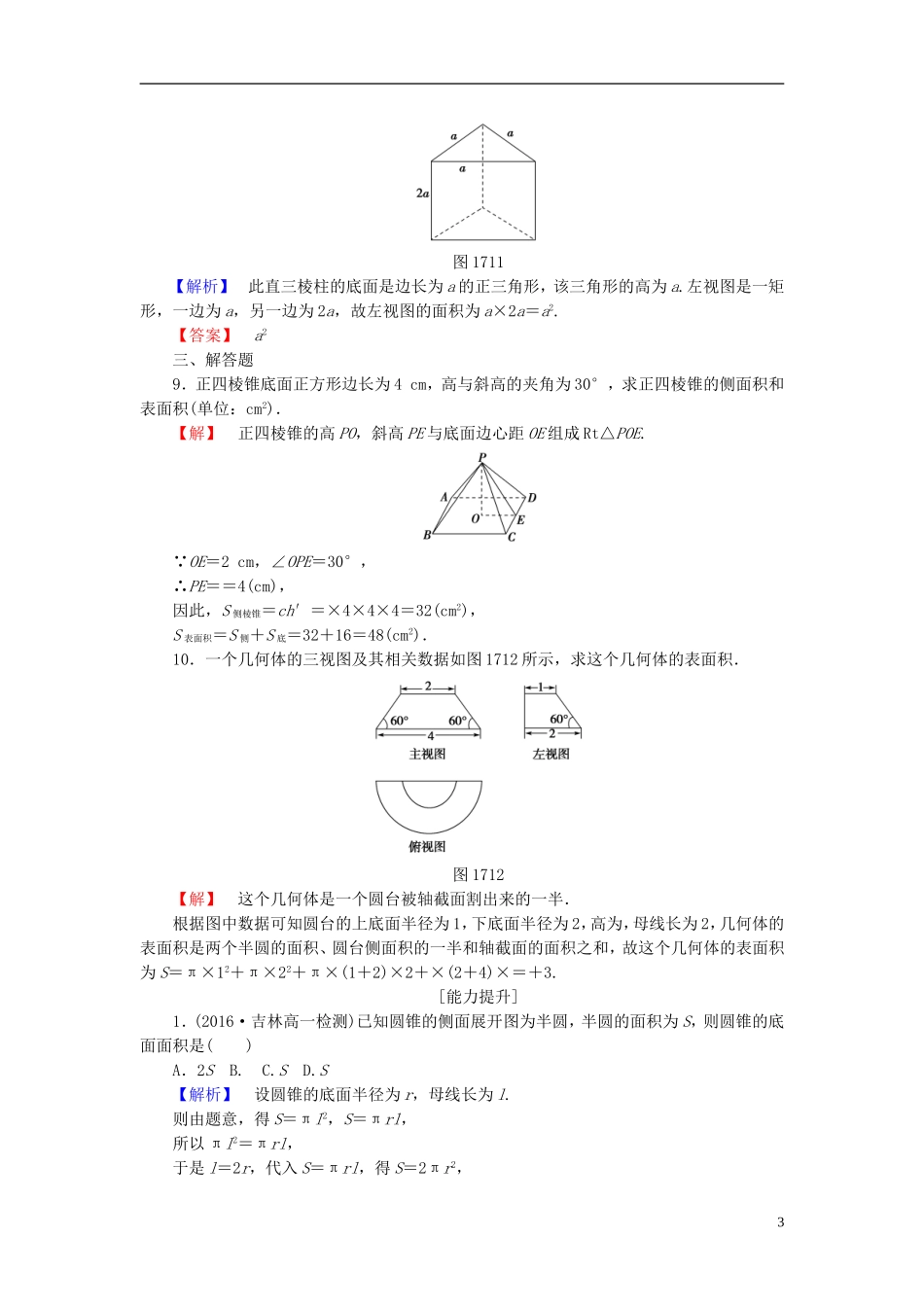
【课堂新坐标】2016-2017学年高中数学第一章立体几何初步学业分层测评10柱、锥、台的侧面展开与面积北师大版必修2(建议用时:45分钟)[学业达标]一、选择题1.一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是直径为1的圆,那么这个几何体的侧面积为()图178A.πB.πC.2πD.3π【解析】由该几何体的三视图可知,其为底面半径为,高为1的圆柱,故S侧=2×π××1=π.【答案】A2.圆台的母线长扩大为原来的n倍,两底面半径都缩小为原来的倍,那么它的侧面积变为原来的()A.1倍B.n倍C.n2倍D.倍【解析】由S侧=π(r′+r)l,当r,r′缩小倍,l扩大n倍时,S侧不变.【答案】A3.某几何体的三视图如图179所示,则该几何体的表面积为()【导学号:10690029】图179A.180B.200C.220D.240【解析】几何体为直四棱柱,其高为10,底面是上底为2,下底为8,高为4,腰为5的等腰梯形,故两个底面面积的和为×(2+8)×4×2=40,四个侧面面积的和为(2+8+5×2)×10=200,所以直四棱柱的表面积为S=40+200=240,故选D.【答案】D4.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是18π,则母线长为()A.2B.3C.4D.2【解析】设圆台的上、下底面圆半径分别为r1,r2,母线长为l,则π(r1+r2)l=18π,即(r1+r2)l=18.1又 l=(r1+r2),∴2l2=18,即l2=9,∴l=3.【答案】B5.(2014·安徽高考)一个多面体的三视图如图1710所示,则该多面体的表面积为()图1710A.21+B.18+C.21D.18【解析】由三视图可知,原几何体是一个正方体截去两个全等的小正三棱锥.正方体的表面积为S=24,两个全等的三棱锥是以正方体的相对顶点为顶点,侧面是三个全等的直角边长为1的等腰直角三角形,其表面积的和为3,三棱锥的底面是边长为的正三角形,其表面积的和为,故所求几何体的表面积为24-3+=21+.【答案】A二、填空题6.已知圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的侧面积为________.【解析】设上底面半径为r,则下底面半径为4r,高为4r, 母线长为10,∴有102=(4r)2+(4r-r)2,解得r=2,∴S圆台侧=π(r+4r)×10=100π.【答案】100π7.侧面都是直角三角形的正三棱锥,底面边长为a,则该三棱锥的表面积为__________.【解析】 底面边长为a,则斜高为,故S侧=3×a×=a2,而S底=a2,故S表=a2.【答案】a28.如图1711,直三棱柱的主视图面积为2a2,则左视图的面积为________.2图1711【解析】此直三棱柱的底面是边长为a的正三角形,该三角形的高为a.左视图是一矩形,一边为a,另一边为2a,故左视图的面积为a×2a=a2.【答案】a2三、解答题9.正四棱锥底面正方形边长为4cm,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积(单位:cm2).【解】正四棱锥的高PO,斜高PE与底面边心距OE组成Rt△POE. OE=2cm,∠OPE=30°,∴PE==4(cm),因此,S侧棱锥=ch′=×4×4×4=32(cm2),S表面积=S侧+S底=32+16=48(cm2).10.一个几何体的三视图及其相关数据如图1712所示,求这个几何体的表面积.图1712【解】这个几何体是一个圆台被轴截面割出来的一半.根据图中数据可知圆台的上底面半径为1,下底面半径为2,高为,母线长为2,几何体的表面积是两个半圆的面积、圆台侧面积的一半和轴截面的面积之和,故这个几何体的表面积为S=π×12+π×22+π×(1+2)×2+×(2+4)×=+3.[能力提升]1.(2016·吉林高一检测)已知圆锥的侧面展开图为半圆,半圆的面积为S,则圆锥的底面面积是()A.2SB.C.SD.S【解析】设圆锥的底面半径为r,母线长为l.则由题意,得S=πl2,S=πrl,所以πl2=πrl,于是l=2r,代入S=πrl,得S=2πr2,3所以圆锥的底面面积πr2=.【答案】B2.(2014·重庆高考)某几何体的三视图如图1713所示,则该几何体的表面积为()图1713A.54B.60C.66D.72【解析】由三视图可知,该几何体为如图所示的一个三棱柱上方被截去一个三棱锥得到的.由三视图中的相关数据易知,底面的面积为×3×4=6,左侧侧面积为3×5=15,前面的侧面积为×(2+5)×4=14,后面的侧面积为×(2+5)×5=,截面积为×3×5=,故表面积为6+14+15++=...