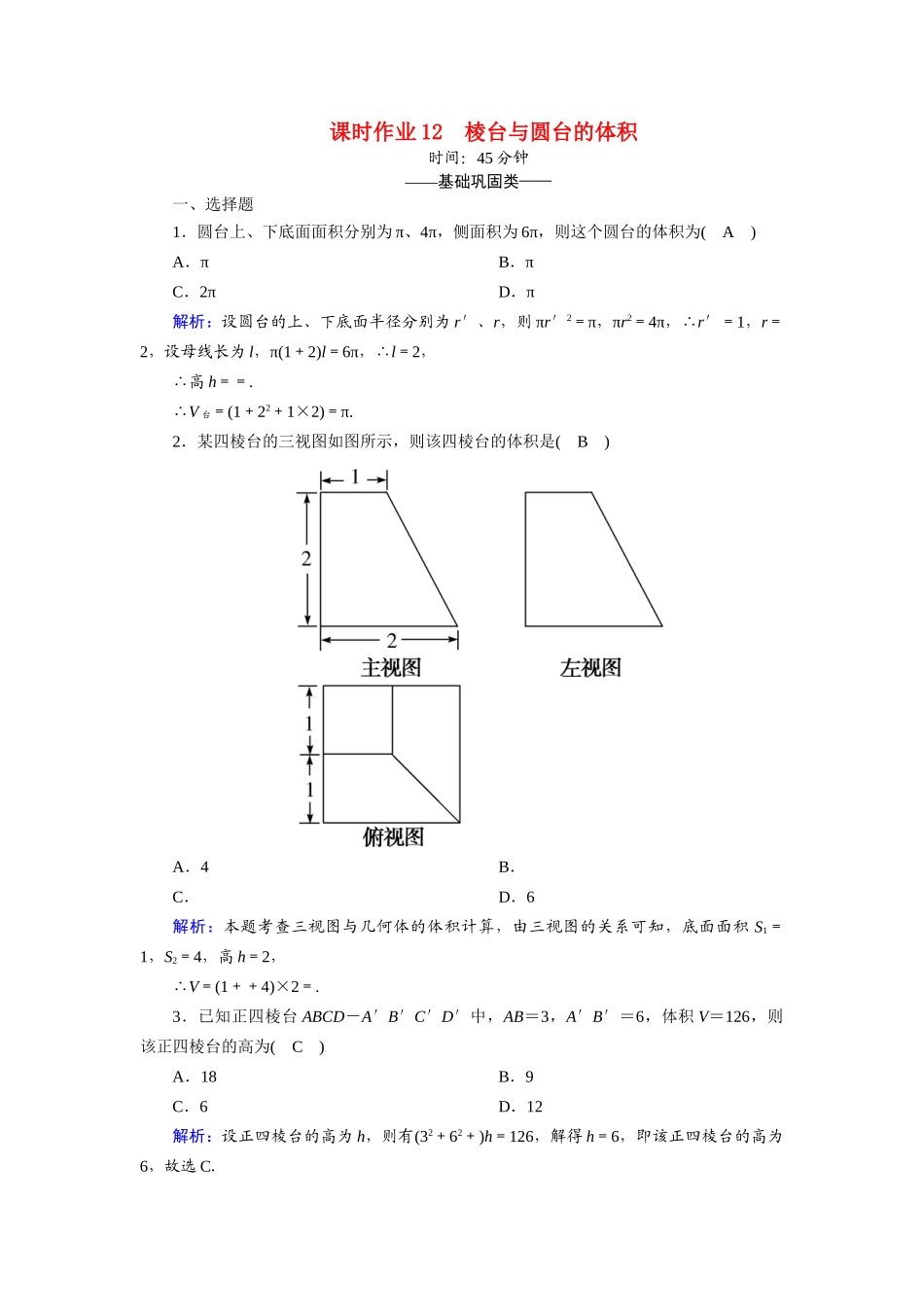
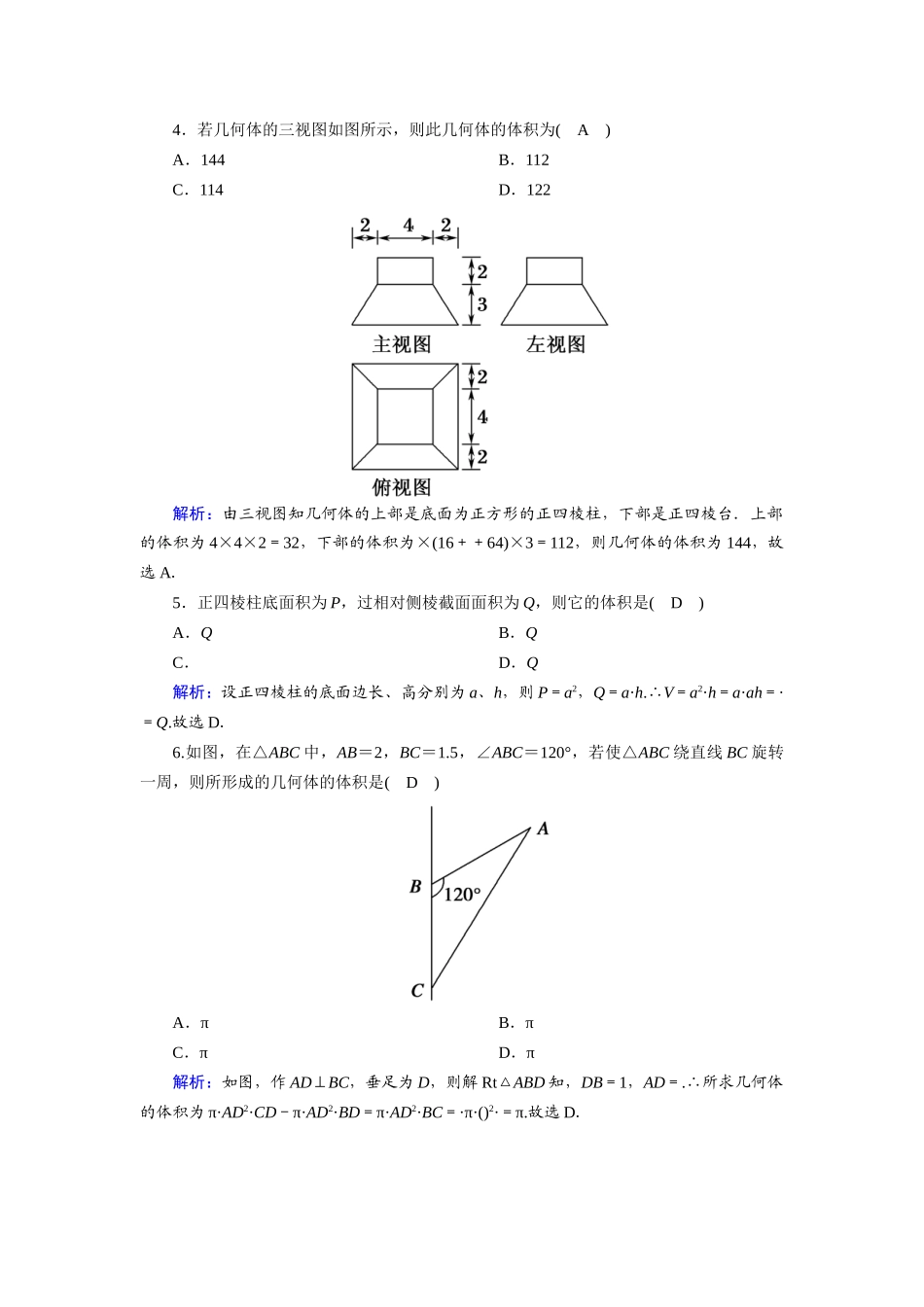
课时作业12棱台与圆台的体积时间:45分钟——基础巩固类——一、选择题1.圆台上、下底面面积分别为π、4π,侧面积为6π,则这个圆台的体积为(A)A.πB.πC.2πD.π解析:设圆台的上、下底面半径分别为r′、r,则πr′2=π,πr2=4π,∴r′=1,r=2,设母线长为l,π(1+2)l=6π,∴l=2,∴高h==.∴V台=(1+22+1×2)=π.2.某四棱台的三视图如图所示,则该四棱台的体积是(B)A.4B.C.D.6解析:本题考查三视图与几何体的体积计算,由三视图的关系可知,底面面积S1=1,S2=4,高h=2,∴V=(1++4)×2=.3.已知正四棱台ABCD-A′B′C′D′中,AB=3,A′B′=6,体积V=126,则该正四棱台的高为(C)A.18B.9C.6D.12解析:设正四棱台的高为h,则有(32+62+)h=126,解得h=6,即该正四棱台的高为6,故选C.4.若几何体的三视图如图所示,则此几何体的体积为(A)A.144B.112C.114D.122解析:由三视图知几何体的上部是底面为正方形的正四棱柱,下部是正四棱台.上部的体积为4×4×2=32,下部的体积为×(16++64)×3=112,则几何体的体积为144,故选A.5.正四棱柱底面积为P,过相对侧棱截面面积为Q,则它的体积是(D)A.QB.QC.D.Q解析:设正四棱柱的底面边长、高分别为a、h,则P=a2,Q=a·h.∴V=a2·h=a·ah=·=Q.故选D.6.如图,在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是(D)A.πB.πC.πD.π解析:如图,作AD⊥BC,垂足为D,则解Rt△ABD知,DB=1,AD=.∴所求几何体的体积为π·AD2·CD-π·AD2·BD=π·AD2·BC=·π·()2·=π.故选D.7.一圆锥的底面半径为4,用平行于底面的截面去截底面半径为1的小圆锥后得到的圆台是原来圆锥体积的(A)A.B.C.D.解析:轴截面如图,由题意==,V圆锥PO1=·PO1,V圆锥PO=π·PO,∴V圆台O1O=V圆锥PO-V圆锥PO1=π·PO-·PO1=π·PO-··PO=π·PO,∴==.(或截得小圆锥底面半径为1,原来底面半径为4,∴相似比为14,故小圆锥与原来大圆锥体积比为164,∴截得圆台与原来大圆锥的体积比为6364.)故选A.8.如图所示,三棱柱ABC-A1B1C1中,若E、F分别为AB、AC的中点,平面EB1C1F将三棱柱分成体积为V1、V2(V1>V2)的两部分,则V1V2等于(C)A.65B.43C.75D.21解析:设三棱柱的高为h,底面的面积为S,体积为V,则V=V1+V2=Sh.因为E、F分别为AB、AC的中点,所以S△AEF=S,V1=h(S+S+)=Sh,V2=Sh-V1=Sh,故V1V2=75.二、填空题9.一个几何体的三视图如图所示,则这个几何体的体积为3.解析:该空间几何体是一个底面为梯形的四棱柱,其底面面积是×2=3,高为1,故其体积为3.10.一个几何体的三视图如图所示(单位:m),则该几何体的体积为30m3.解析:本题考查三视图及柱体体积公式.由三视图知该几何体由一个棱长为3,4,2的长方体和一个底面是直角梯形且高为4的直棱柱组成,则体积V=3×4×2+×1×4=30,解决三视图问题应弄清图中各量与原几何体的量的关系.11.若一个圆台的轴截面是腰长为a的等腰梯形,下底边长为2a,对角线长为a,则这个圆台的体积为πa3.解析:圆台的轴截面如图,由AD=a,AB=2a,BD=a,可知∠ADB=90°.分别过D,C作DH⊥AB,CG⊥AB,所以DH=a,AH=,所以HB===a,所以DC=HG=a,所以圆台的体积为V=π··a=πa3.三、解答题12.棱台的体积为76cm3,高6cm,一个底面的面积为18cm2,求另一个底面的面积.解:设另一个底面面积为xcm2,则由V=h(S上+S下+),得76=×6×(18+x+),解得x=8,∴另一个底面面积是8cm2.13.设圆台的高为3,其轴截面(过圆台轴的截面)如图所示,母线A1A与底面圆的直径AB的夹角为60°,在轴截面中A1B⊥A1A,求圆台的体积V.解:如图,设AB的中点为O,连接A1O,作A1D⊥AB,易知A1D=3,因A1B⊥A1A,则在Rt△A1AB中,A1O=AB=AO.又因为∠A1AB=60°,所以△A1AO为等边三角形.所以在△A1AO中,A1D=AO=3,得AO=2.设圆台的上、下底面半径分别为r,R.所以R=AO=2,r=A1B1=OB=AO=DO=.则V=π×3×(12+2×+3)=π×(12+6+3)=21π.故圆台体积为21...