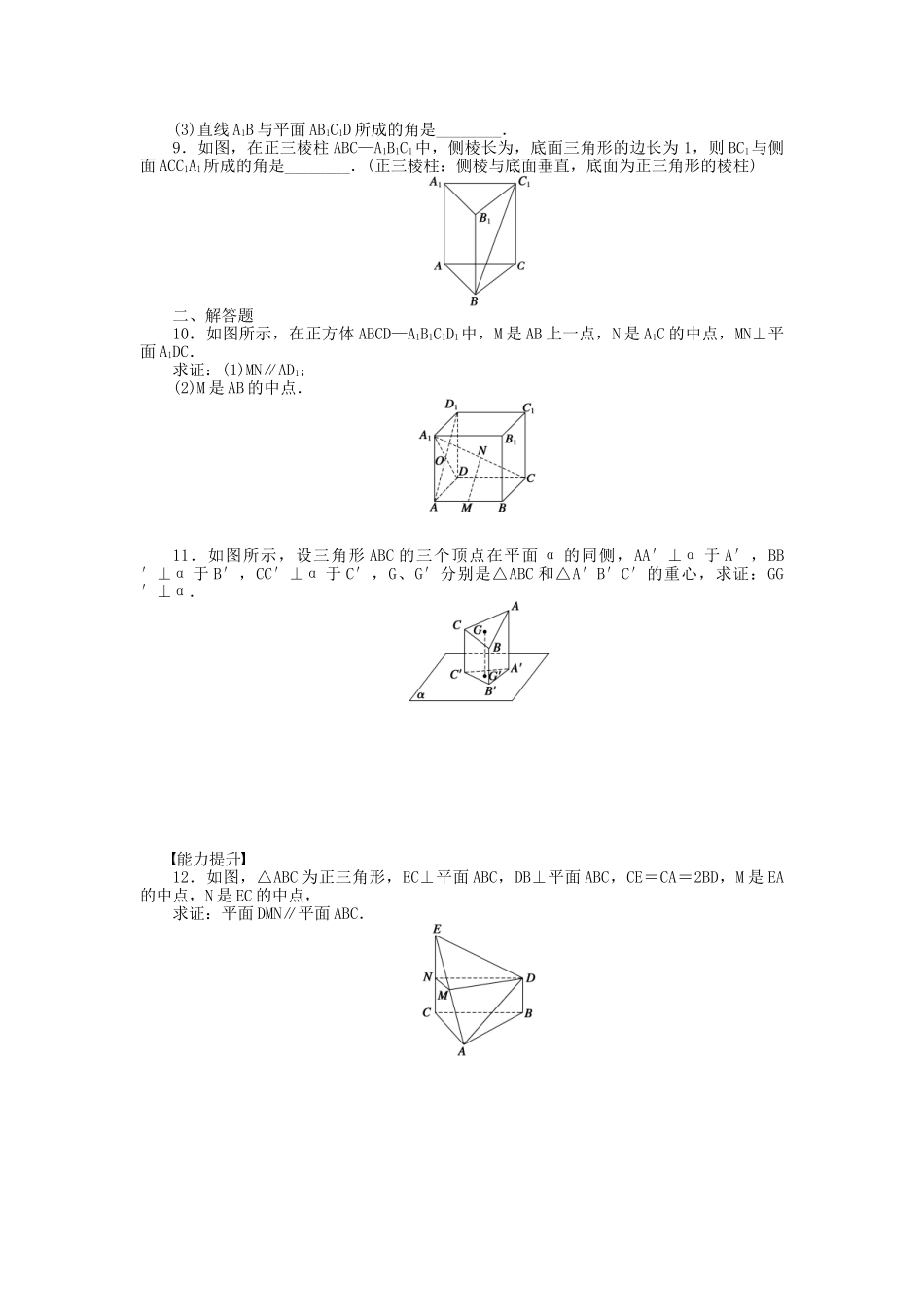
第4课时直线与平面垂直的性质【课时目标】1.掌握直线与平面垂直的性质定理.2.会求直线与平面所成的角.1.直线与平面垂直的性质定理:如果两条直线垂直于同一个平面,那么这两条直线________.该定理用图形表示为:用符号表示为:________________________.2.直线和平面的距离:一条直线和一个平面________,这条直线上______________到这个平面的距离,叫做这条直线和这个平面的距离.3.平面的一条斜线与它在这个平面内的射影所成的锐角,叫做这条直线与这个平面______________.规定:若直线与平面垂直,则直线与平面所成的角是________.若直线与平面平行或直线在平面内,则直线与平面所成的角是________的角.一、填空题1.与两条异面直线同时垂直的平面有________个.2.若m、n表示直线,α表示平面,则下列命题中,正确命题的个数为________.①⇒n⊥α;②⇒m∥n;③⇒m⊥n;④⇒n⊥α.3.已知直线PG⊥平面α于G,直线EF⊂α,且PF⊥EF于F,那么线段PE,PF,PG的大小关系是______________.4.PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任一点,则下列关系正确的是________(填序号).①PA⊥BC;②BC⊥平面PAC;③AC⊥PB;④PC⊥BC.5.P为△ABC所在平面外一点,O为P在平面ABC内的射影.(1)若P到△ABC三边距离相等,且O在△ABC的内部,则O是△ABC的________心;(2)若PA⊥BC,PB⊥AC,则O是△ABC的______心;(3)若PA,PB,PC与底面所成的角相等,则O是△ABC的________心.6.线段AB在平面α的同侧,A、B到α的距离分别为3和5,则AB的中点到α的距离为________.7.直线a和b在正方体ABCD-A1B1C1D1的两个不同平面内,使a∥b成立的条件是________.(只填序号)①a和b垂直于正方体的同一个面;②a和b在正方体两个相对的面内,且共面;③a和b平行于同一条棱;④a和b在正方体的两个面内,且与正方体的同一条棱垂直.8.在正方体ABCD-A1B1C1D1中,(1)直线A1B与平面ABCD所成的角是________;(2)直线A1B与平面ABC1D1所成的角是________;(3)直线A1B与平面AB1C1D所成的角是________.9.如图,在正三棱柱ABC—A1B1C1中,侧棱长为,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是________.(正三棱柱:侧棱与底面垂直,底面为正三角形的棱柱)二、解答题10.如图所示,在正方体ABCD—A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.求证:(1)MN∥AD1;(2)M是AB的中点.11.如图所示,设三角形ABC的三个顶点在平面α的同侧,AA′⊥α于A′,BB′⊥α于B′,CC′⊥α于C′,G、G′分别是△ABC和△A′B′C′的重心,求证:GG′⊥α.能力提升12.如图,△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.13.如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.(1)求证:MN⊥平面A1BC;(2)求直线BC1和平面A1BC所成的角的大小.1.直线和平面垂直的性质定理可以作为两条直线平行的判定定理,可以并入平行推导链中,实现平行与垂直的相互转化,即线线垂直⇒线面垂直⇒线线平行⇒线面平行.2.求线面角,确定直线在平面内的射影的位置,是解题的关键.因为只有确定了射影的位置,才能找到直线与平面所成的角,才能将空间的问题转化为平面的问题来解.第4课时直线与平面垂直的性质答案知识梳理1.平行a⊥α,b⊥α⇒a∥b2.平行任意一点3.所成的角直角0°作业设计1.02.3解析①②③正确,④中n与面α可能有:n⊂α或n∥α或相交(包括n⊥α).3.PE>PF>PG解析由于PG⊥平面α于G,PF⊥EF,∴PG最短,PF
PF>PG.4.①②④解析PA⊥平面ABC,得PA⊥BC,①正确;又BC⊥AC,∴BC⊥面PAC,∴BC⊥PC,②、④均正确.5.(1)内(2)垂(3)外6.4解析由直线与平面垂直的性质定理知AB中点到α距离为以3和5为上、下底的直角梯形的中位线的长.7.①②③解析①为直线与平面垂直的性质定理的应用,②为面面平行的性质,③为公理4的应用.8.(1)45°(2)30°(3)90°解析(1)由线面角定义知∠A1BA为A1B与平面ABCD所成的角,∠A1BA=45°.(2)连结A1D、AD1,交点为O,则易证A1D⊥...