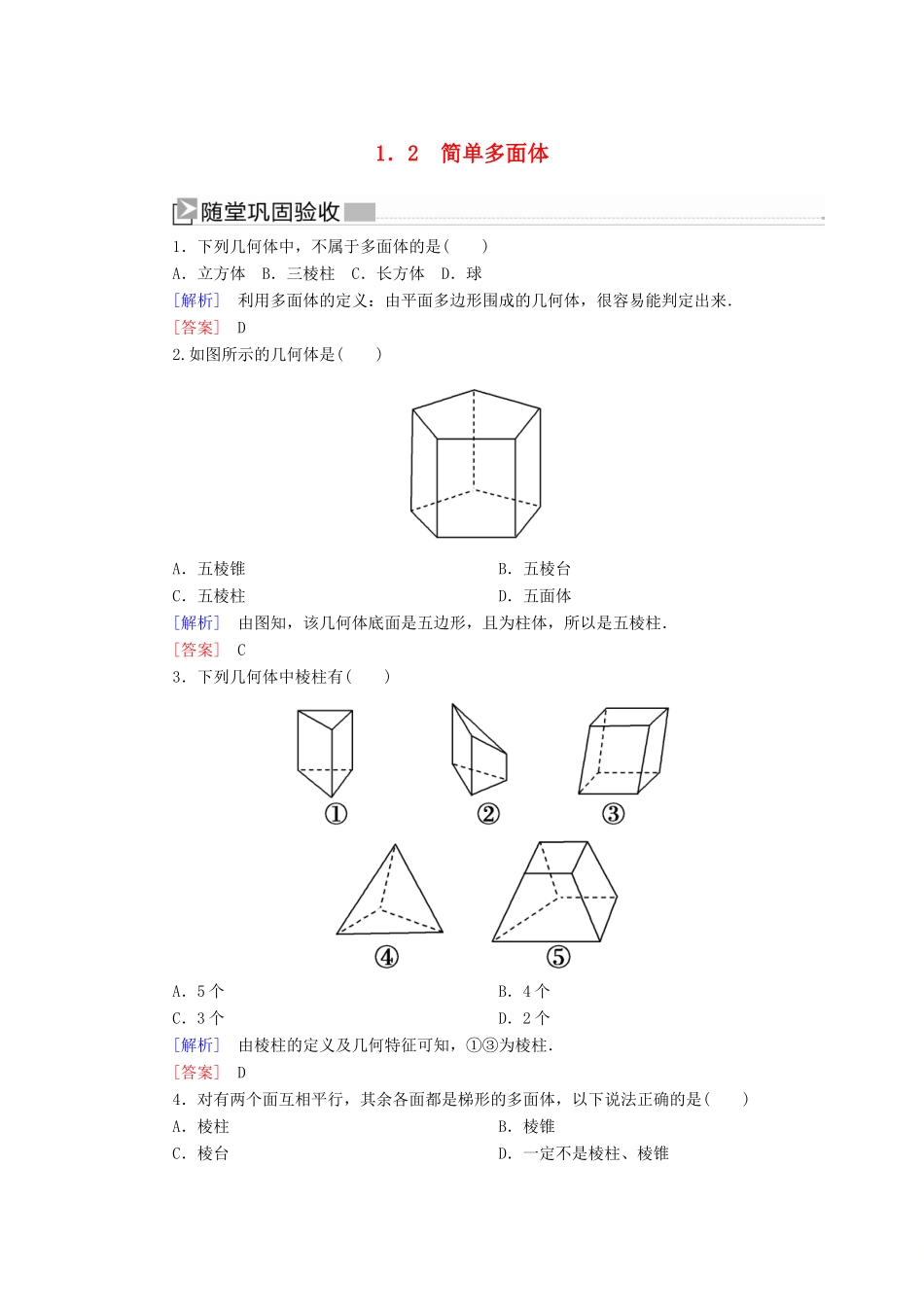
1.2简单多面体1.下列几何体中,不属于多面体的是()A.立方体B.三棱柱C.长方体D.球[解析]利用多面体的定义:由平面多边形围成的几何体,很容易能判定出来.[答案]D2.如图所示的几何体是()A.五棱锥B.五棱台C.五棱柱D.五面体[解析]由图知,该几何体底面是五边形,且为柱体,所以是五棱柱.[答案]C3.下列几何体中棱柱有()A.5个B.4个C.3个D.2个[解析]由棱柱的定义及几何特征可知,①③为棱柱.[答案]D4.对有两个面互相平行,其余各面都是梯形的多面体,以下说法正确的是()A.棱柱B.棱锥C.棱台D.一定不是棱柱、棱锥[解析]根据棱柱、棱锥、棱台的特征可知,一定不是棱柱、棱锥.[答案]D多面体表面距离最短问题表面距离最短问题,一般方法是展成平面图形,利用两点间距离最短来解决.【示例】如图①所示,在侧棱长为2的正棱锥V-ABC中(底面为正三角形,过顶点与底面垂直的直线过底面的中心),∠AVB=∠BVC=∠CVA=40°,过A作截面△AEF,求截面△AEF周长的最小值.[思路分析]把正三棱锥的侧面展开成平面图形,当△AEF的各边在同一直线上时,其周长最小.[解]将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图②所示,线段AA1的长为所求△AEF周长的最小值,取AA1的中点D,则VD⊥AA1,∠AVD=60°,可求AD=3,则AA1=6.[题后反思]有关几何体的距离的最值问题有两类基本方法:(1)函数思想:设出变量,把所求距离写成关于变量的函数表达式,再利用函数方法求最值.(2)转化思想:通过表面展开,转化为平面问题变曲为直,利用几何性质求解.[针对训练]某城市中心广场主题建筑为一三棱锥,且所有边长均为10m,如图所示,其中E,F分别为AD,BC的中点.(1)画出该几何体的表面展开图,并注明字母;(2)为迎接国庆,城管部门拟对该建筑实施亮化工程,现预备从底边BC中点F处分别过AC,AB上某点向AD中点E处架设LED灯管,所用灯管长度最短为多少?[解](1)该几何体的表面展开图如图所示(2)由该几何体的展开图知,四边形ACBD为菱形,四边形ABCD为菱形.若使由F向E所架设灯管长度最短,可由其展开图中连接线段EF.这两条线段均为10,故所用灯管最短为20m.