18.1勾股定理VIP免费

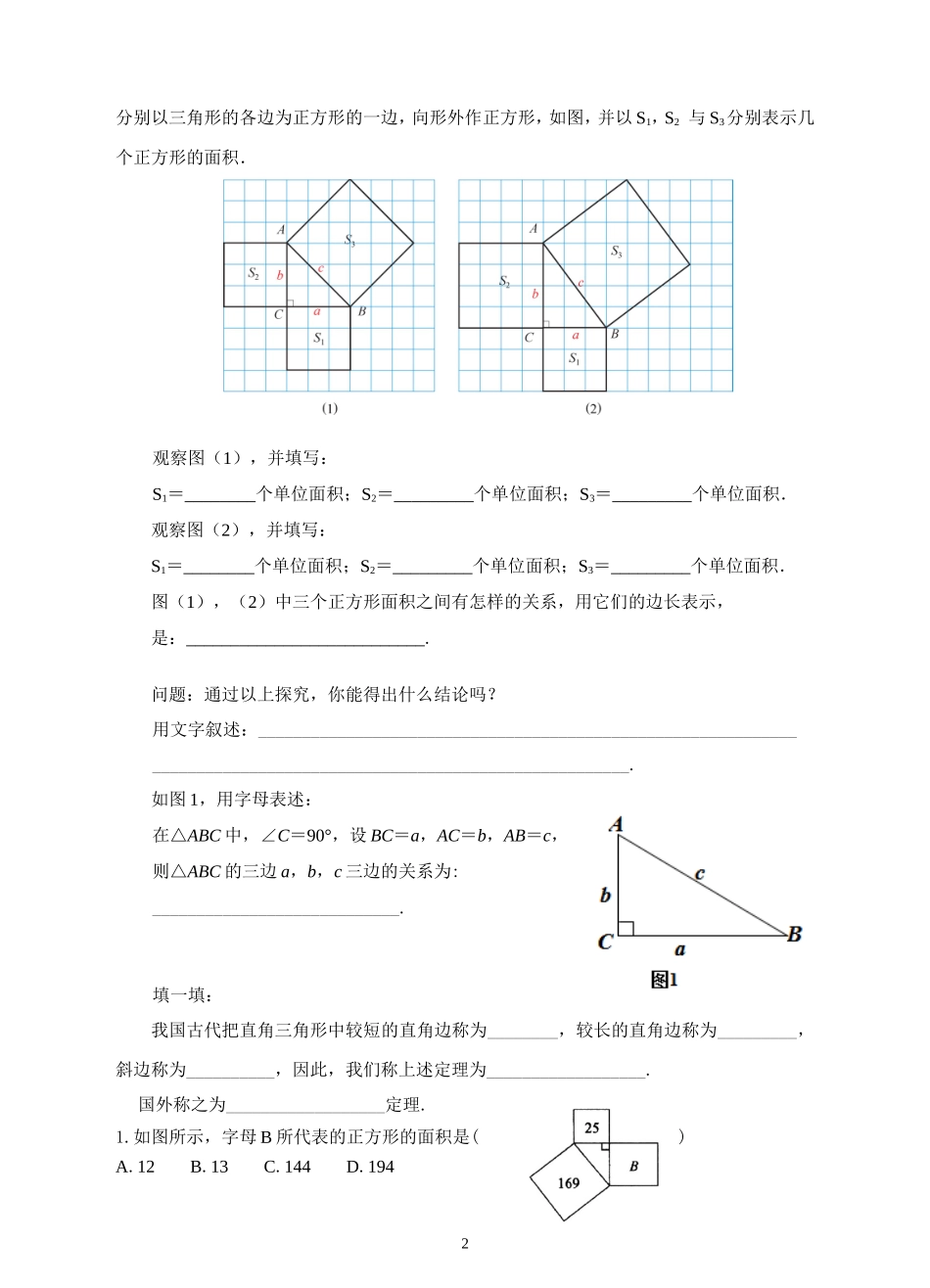
118.1《勾股定理》第一课时导学案学习目标1.了解勾股定理的由来；2.探索直角三角形的三边之间关系，了解利用拼图验证勾股定理的方法；3.掌握勾股定理并会用它解决身边与实际生活相关的数学问题.学习重难点重点：探索和验证勾股定理的过程；难点：通过面积计算探索勾股定理.学法指导通过勾股定理的探究和验证，学会用直角三角形的三边关系解决实际问题.学习过程一、课前自习，温故知新1.查找相关资料或上网查找有关勾股定理的由来.（1）勾股定理是一个基本的几何定理，它在许多领域都有着广泛的应用，国内外都有很多科学家、知名人士对此都有过研究，至今已有400多种证明方法。（2）国内：公元十一世纪周朝数学家就提出“勾三股四弦五”，在《周髀算经》中有所记载。公元3世纪三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，创制了一幅“勾股圆方图”，把勾股定理叙述成：勾股各自乘，并之为弦实，开方除之即弦。（3）国外：公元前六世纪，希腊数学家毕达哥拉斯(Pythagoras)证明了勾股定理，因而西方人都习惯地称这个定理为毕达哥拉斯定理。公元前4世纪，希腊数学家欧几里得在巨著《几何原本》（第Ⅰ卷，命题47）中给出一个很好的证明。1876年4月1日，加菲乐德在《新英格兰教育日志》上发表了他对勾股定理的一个证法。www.21-cn-jy.二、课前探究，交流学习1.探究1：在行距、列距都是1的方格网中，任意作出几个以格点为顶点的直角三角形，2分别以三角形的各边为正方形的一边，向形外作正方形，如图，并以S1，S2与S3分别表示几个正方形的面积．2·1·c·n·j·y观察图（1），并填写：S1＝________个单位面积；S2＝_________个单位面积；S3＝_________个单位面积．观察图（2），并填写：S1＝________个单位面积；S2＝_________个单位面积；S3＝_________个单位面积．图（1），（2）中三个正方形面积之间有怎样的关系，用它们的边长表示，是：___________________________.问题：通过以上探究，你能得出什么结论吗？用文字叙述：___________________________________________________________________________________________________________________.21·cn·jy·com如图1，用字母表述：在△ABC中，∠C＝90°，设BC＝a，AC＝b，AB＝c，则△ABC的三边a，b，c三边的关系为:____________________________.填一填：我国古代把直角三角形中较短的直角边称为________，较长的直角边称为_________，斜边称为__________，因此，我们称上述定理为__________________.国外称之为__________________定理.1.如图所示，字母B所代表的正方形的面积是()A.12B.13C.144D.19432.一个直角三角形，两直角边长分别为3和4，下列说法正确的是()A.斜边长为25B.三角形的周长为25C.斜边长为5D.三角形面积为203.已知正方形原边长为a，则正方形的对角线的长度为（）A.2aB.aC.aD.a4.在Rt△ABC中，∠C＝90°，AC＝8，△ABC的面积为24，则斜边AB的长为（）A.6B.8C.10D.125.一直角三角形的两边长分别为3和4，则第三边长为（）A.5B.C.D.5或6.如图，山坡AB的高BC＝5m，水平距离AC＝12m，若在山坡上每隔0.65m栽一棵树（两头各栽一棵），则从上到下共栽（）21cnjy.comA.19棵B.20棵C.21棵D.22棵7.要登上8m高的建筑物，为了安全需要，需使梯子底端离建筑物6m，至少需要多长的梯子?8.如图所示，从电线杆离地面6m处向地面拉一条长10m的缆绳，这条缆绳在地面的固定点距离电线杆底部有多远.