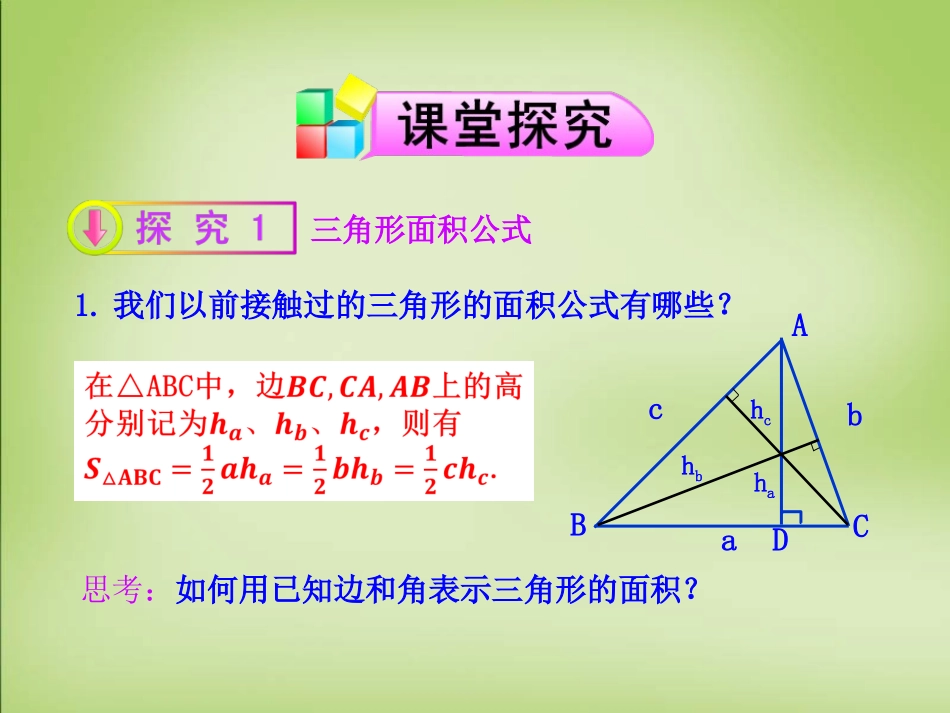
第3课时三角形中的几何计算1.能够运用正弦定理、余弦定理等知识和方法进一步解决有关三角形的问题,掌握三角形的面积公式的简单推导和应用;(重点)2.三角形各种类型的判定方法.1.我们以前接触过的三角形的面积公式有哪些?D思考:如何用已知边和角表示三角形的面积?三角形面积公式AaCBcbhahchb2.已知边角求三角形的面积:ha=bsinC=csinBhb=csinA=asinChc=asinB=bsinAAahaCBDcb分析:这是一道在不同的已知条件下求三角形的面积的问题,与解三角形问题有密切的关系,我们可以应用解三角形面积的知识,观察已知什么,尚缺什么,求出需要的元素,就可以求出三角形的面积.(3)根据余弦定理的推论,得,例2如图,某市在进行城市环境建设中,要把一个三角形的区域改造成市内公园,经过测量得到这个三角形区域的三条边长分别为68m,88m,127m,这个区域的面积是多少?(精确到0.1㎡)分析:本题可转化为已知三角形的三边,求角的问题,再利用三角形的面积公式求解。CAB解:设a=68m,b=88m,c=127m,根据余弦定理的推论,,得,..例3在△ABC中,求证:分析:这是一道关于三角形边角关系恒等式的证明问题,观察式子左右两边的特点,联想到用正弦定理和余弦定理来证明.三角形边角关系应用证明:(1)根据正弦定理,可设,;(2)根据余弦定理,右边=(b2+c2-a2)+(c2+a2-b2)+(a2+b2-c2)=a2+b2+c2=左边.(1)acosA=bcosB;例4判断满足下列条件的三角形的形状.提示:利用正弦定理或余弦定理,“化边为角”或“化角为边”.判断三角形的形状另解:由正弦定理得sinAcosA=sinBcosB,所以sin2A=sin2B,即2A=2B,根据边的关系易得是等腰三角形.所以A=B,思考:为什么两种求解方法答案不同,哪个正确?哪个错误?为什么?因为sin2A=sin2B,有可能推出2A与2B两个角互补,即2A+2B=180°,则A+B=90°.前一种解法正确.后一种解法遗漏了一种情况;,,,,,所以此三角形为直角三角形.利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,从而确定三角形的形状.特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用.答:三角形的面积为333-3.22或4.(2012·新课标全国高考)已知a,b,c分别为△ABC三个内角A,B,C的对边,cos3sin0aCaCbc(1)求A;(2)若a=2,△ABC的面积为,求b,c.3解析:(1)由及正弦定理得cos3sin0aCaCbcsincos3sinsinsinsin0ACACBC,BAC3sincoscossinsin0ACACC由于sinC≠0,所以1sin().62A又0