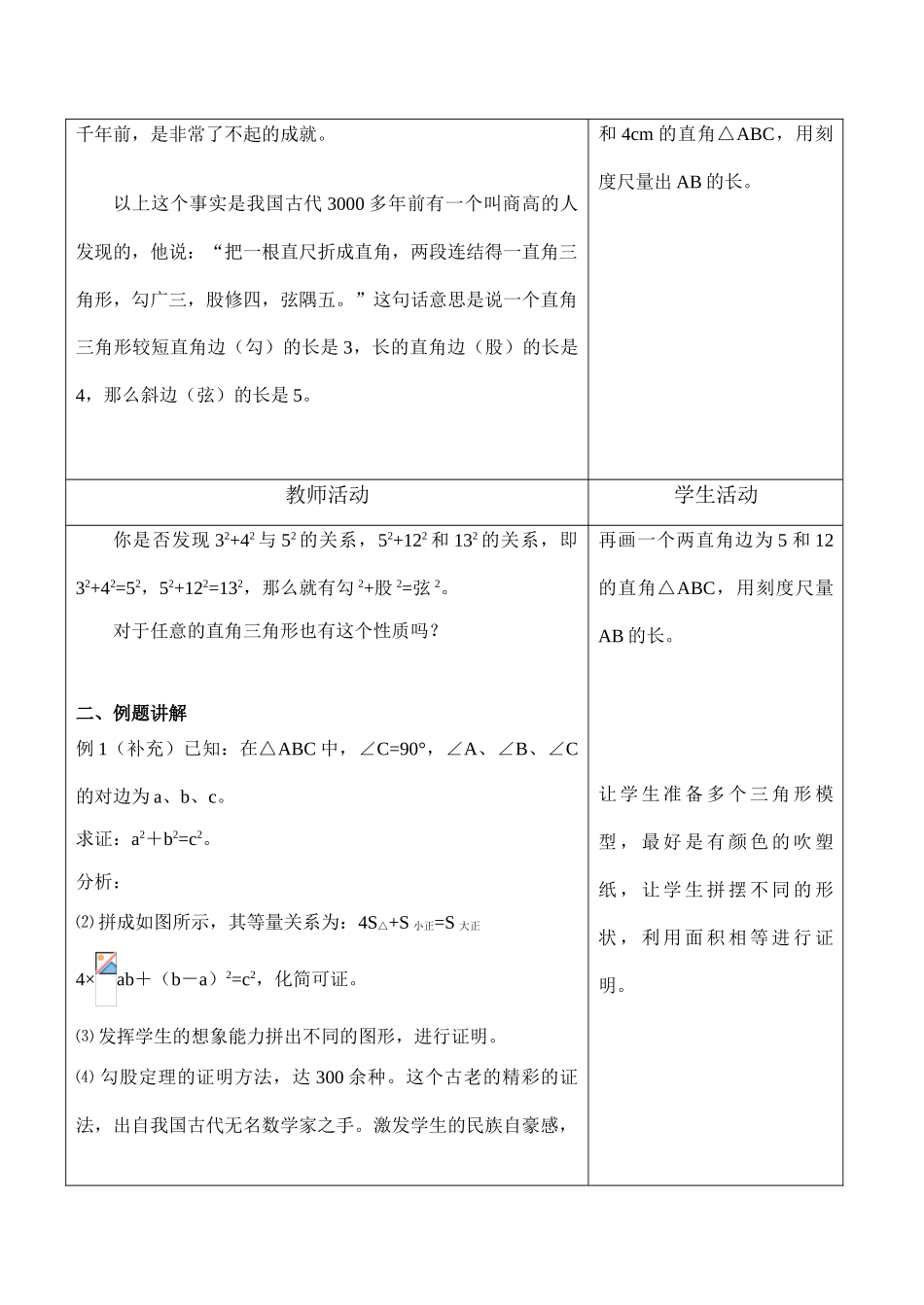
八年级数学勾股定理一、教学任务分析:课题18.1勾股定理(一)课型新授课教学目标知识与技能1.知道勾股定理的发现过程,知道勾股定理的内容,会用面积法证明勾股定理。过程与方法培养在实际生活中发现问题总结规律的意识和能力。情感目标介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习。教学重点与难点1.重点:勾股定理的内容及证明。2.难点:勾股定理的证明。教学资源小黑板预习作业内容1、阅读书本P72~742、完成自主练习与检测的基础平台时间15分钟方法通过阅读自学。要求认真阅读,领会勾股定理的内容及证明方法二、教学过程设计:教师活动学生活动一、课堂引入目前世界上许多科学家正在试图寻找其他星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言、音乐、各种图形等。我国数学家华罗庚曾建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的。这个事实可以说明勾股定理的重大意义。尤其是在两让学生画一个直角边为3cm千年前,是非常了不起的成就。以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五。”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5。和4cm的直角△ABC,用刻度尺量出AB的长。教师活动学生活动你是否发现32+42与52的关系,52+122和132的关系,即32+42=52,52+122=132,那么就有勾2+股2=弦2。对于任意的直角三角形也有这个性质吗?二、例题讲解例1(补充)已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。分析:⑵拼成如图所示,其等量关系为:4S△+S小正=S大正4×ab+(b-a)2=c2,化简可证。⑶发挥学生的想象能力拼出不同的图形,进行证明。⑷勾股定理的证明方法,达300余种。这个古老的精彩的证法,出自我国古代无名数学家之手。激发学生的民族自豪感,再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长。让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明。和爱国情怀。例2已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2。分析:左右两边的正方形边长相等,则两个正方形的面积相等。左边S=4×ab+c2,右边S=(a+b)2,左边和右边面积相等,即4×ab+c2=(a+b)2教师活动学生活动三、课堂练习1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)⑴两锐角之间的关系:;⑵若D为斜边中点,则斜边中线;⑶若∠B=30°,则∠B的对边和斜边:;⑷三边之间的关系:。2.△ABC的三边a、b、c,若满足b2=a2+c2,则=90°;若满足b2>c2+a2,则∠B是角;若满足b2<c2+a2,则∠B是角。4.根据如图所示,利用面积法证明勾股定理。课堂总结1.勾股定理的内容2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则⑴c=。(已知a、b,求c)⑵a=。(已知b、c,求a)⑶b=。(已知a、c,求b)三、作业布置:P77~78/1~5四、教后反思:启东市双鹤学校个人备课教案一、教学任务分析:课题18.1勾股定理(二)课型新授课教学目标知识与技能1.会用勾股定理进行简单的计算。2.树立数形结合的思想、分类讨论思想。过程与方法通过学生画好图形,标好图形,理清边边之间的关系,明确在直角三角形中,已知任意两边都可以求出第三边,学会利用不同的条件转化为已知两边求第三边。情感目标注意所给条件的不确定性,知道考虑问题要全面,体会分类讨论思想。教学重点与难点1.重点:勾股定理的简单计算。2.难点:勾股定理的灵活运用。教学资源小黑板预习作业内容完成自主练习与检测页的基础平台时间15分钟方法自学。要求会应用勾股定理解决预习作业二、教学过程设计:教师活动学生活动一、课堂引入复习勾股定理的文字叙述;勾股定理的符号语言及变形。学习勾股定理重在应用。二、、例习题分析例1(补充)在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知a=1,c=2,求b。⑶已知c=17,b=8,求a。⑷已知a:b=1:2,c=5,求a。⑸已知b=15,...