【课堂新坐标】2013届高三数学一轮复习-第3章第8节-正弦定理、余弦定理的应用举例课件-文-(广东专用)VIP免费

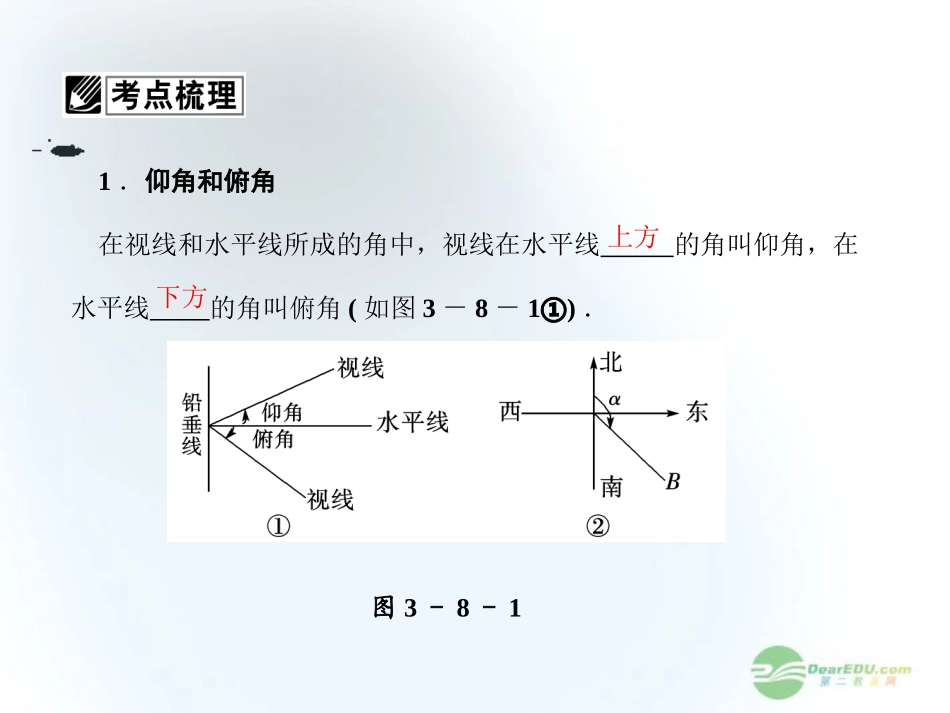
第八节正弦定理、余弦定理的应用举例1．仰角和俯角在视线和水平线所成的角中，视线在水平线的角叫仰角，在水平线的角叫俯角(如图3－8－1①)．图3－8－1上方下方2．方位角和方向角(1)方位角：从指北方向转到目标方向线的水平角，如B点的方位角为α(如图3－8－1②)(2)方向角：相对于某正方向的水平角，如南偏东30°等．3．坡度与坡比坡度：坡面与水平面所成的二面角的度数．坡比：坡面的铅直高度与水平长度之比．顺时针如何用方位角、方向角确定一点的位置？【提示】利用方位角或方向角和目标与观测点的距离即可唯一确定一点的位置．1．(教材改编题)如图3－8－2所示，已知两座灯塔A和B与海洋观察站C的距离都等于akm，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为()A．akmB.3akmC.2akmD．2akm图3－8－2【解析】在△ABC中，AC＝BC＝a，∠ACB＝120°，∴AB2＝a2＋a2－2a2cos120°＝3a2，AB＝3a.【答案】B图3－8－3【答案】2sinα－2cosα＋2【解析】三角形的底边长为x＝1＋1－2×1×1×cosα＝2－2cosα，∴S＝4S△＋S正方形＝4×12×1×1×sinα＋x2＝2sinα＋2－2cosα＝2sinα－2cosα＋2.2．某班设计了一个八边形的班徽(如图3－8－3)，它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为________．3．(2011·上海高考)在相距2千米的A、B两点处测量目标点C，若∠CAB＝75°，∠CBA＝60°，则A、C两点之间的距离为________千米．【解析】在△ABC中，∠CAB＝75°，∠CBA＝60°，∴∠ACB＝180°－75°－60°＝45°，又AB＝2，由正弦定理，得ACsin60°＝ABsin45°，故AC＝6.【答案】6图3－8－44.2010年10月21日超强风暴“鲇鱼”导致台湾“苏花高速”坍塌，在灾区的搜救现场(如图3－8－4所示)，一条搜救狗从A处沿正北方向行进xm到达B处发现一个生命迹象，然后向右转105°，行进10m到达O处发现另一生命迹象，这时它向右转135°后继续前进可回到出发点，那么x＝________.【解析】依题意，在△AOB中，β＝45°，A＝60°，OB＝10，由正弦定理，xsin45°＝10sin60°，故x＝1036.【答案】1036如图3－8－5所示，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB＝90°，BD交AC于E，AB＝2.(1)求cos∠CBE的值；(2)求AE.图3－8－5【思路点拨】(1)在△BCD中，利用等腰三角形的性质求∠CBE；(2)在ABE中，利用正弦定理求AE.【尝试解答】(1)因为∠BCD＝90°＋60°＝150°，CB＝AC＝CD，所以∠CBE＝15°，所以cos∠CBE＝cos(45°－30°)＝6＋24.(2)在△ABE中，AB＝2，由正弦定理AEsin45°－15°＝2sin90°＋15°，故AE＝2sin30°cos15°＝1cos15°＝6－2.,(2011·安徽高考)在△ABC中，a，b，c分别为内角A，B，C所对的边长，a＝3，b＝2，1＋2cos(B＋C)＝0，求边BC上的高．【解】由1＋2cos(B＋C)＝0和B＋C＝π－A，得1－2cosA＝0，所以cosA＝12，所以sinA＝32.再由正弦定理，得sinB＝bsinAa＝22.由b＜a知B＜A，所以B不是最大角，B＜π2，从而cosB＝1－sin2B＝22.由上述结果知sinC＝sin(A＋B)＝22(32＋12)．设边BC上的高为h，则h＝bsinC＝3＋12.所以边BC上的高为3＋12.,(2012·韶关质检)如图3－8－6所示，测量河对岸的塔高AB时，可选取与塔底B在同一水平面内的两个测点C与D，现测得∠BCD＝75°，∠BDC＝60°，CD＝s，并在点C处测得塔顶A的仰角为30°，求塔高AB.【思路点拨】在△BCD中，求CB；在△ACB中，求AB.图3－8－6【尝试解答】在△BCD中，∠CBD＝180°－75°－60°＝45°，由正弦定理得BCsin∠BDC＝CDsin∠CBD，所以BC＝CD·sin∠BDCsin∠CBD＝s·sin60°sin45°＝62s.在Rt△ABC中，AB＝BC·tan∠ACB＝62s·tan30°＝22s.因此塔高为22s.,某人在C点测得某塔在南偏西80°，塔顶A仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，求该塔的高度．【解】如图所示，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h，在Rt△AOD中，∠ADO＝30°，∴OD＝3·OA＝3h，在△OCD中，CD＝10，且∠OCD＝120°，由余弦定理得：OD2＝OC2＋CD2－2OC·CDcos∠OCD，即(3h)2＝h2＋102－2h×10×cos120°，∴h2－5h－...