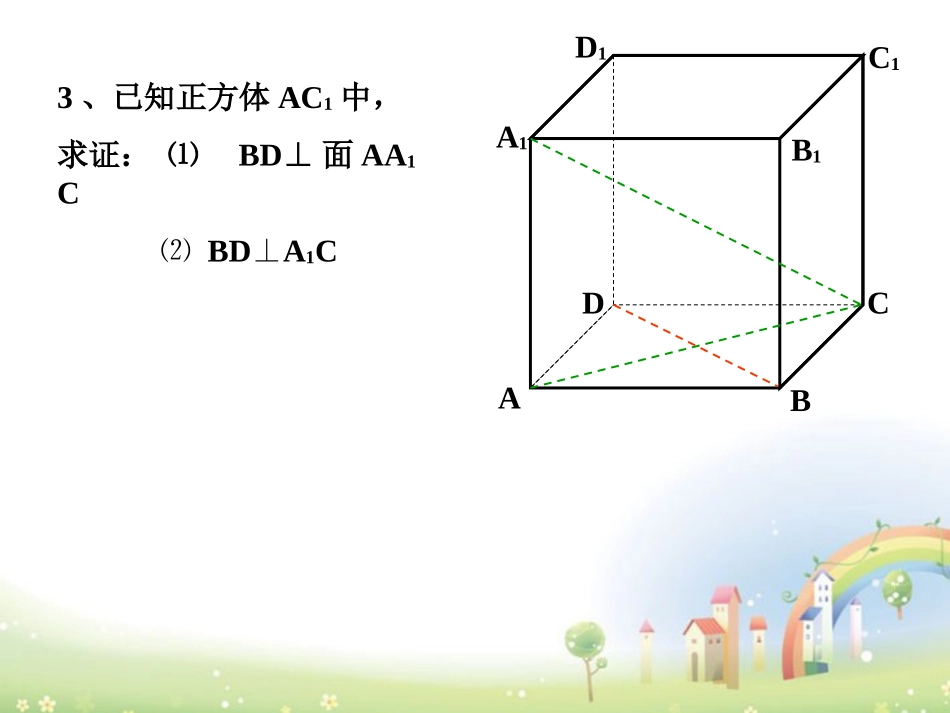
三垂线定理复习巩固1、直线和平面垂直的判定定理为2、①过平面外一点向这个平面引垂线,垂足叫做这个点在这个平面内的。②一条直线和一个平面相交,但不和这个平面垂直,那么这条直线叫做这个平面的。③从斜线上斜足以外的一点向平面引垂线,经过垂足和斜足的直线叫。如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面射影斜线直线在平面上的射影3、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D113、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D13、已知正方体AC1中,求证:⑴BD⊥面AA1C⑵BDA⊥1CABCDA1B1C1D1证明:证明:⑴在正方体AC1中,AA1⊥面ABCDAA1BD∴⊥又BDACAC∩AA1=A⊥∴BD⊥面AA1C⑵由⑴知BD⊥面AA1CA1C在面AA1CBD∴A1C⊥4、在正方体AC1中,AC1在平面ABCD、BB1C1C内的射影分别()平面ABCD、BB1C1C内的直线BD、BC1分别与对应的斜线是否垂直?与对应的射影呢?ABCDA1B1C1D1AC、B1C垂直POAaα在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。已知:PO、PA分别是平面α的垂线、斜线,OA是PA在平面α内的射影,且a在平面α内,aOA⊥求证:aPA⊥三垂线定理证明:∵PO⊥平面α垂且a在平面α内∴POa⊥又aOAOA⊥∩PO=Oa∴⊥面PAO∴aPA⊥注意关键:⑴寻找“垂面”⑵确定“射影”⑶判别“垂直”三线:斜线、射影、面内一条直线三垂线定理的逆定理在平面内的一条直线、如果它和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。三垂线定理及其逆定理符号:al⊥al′⊥ABCDA1B1C1D1FE已知:如图,正方体AC1中,E、F分别为棱AB、BC的中点求证:C1EDF⊥例:证明:正方形ABCD中,E、F分别为AB、BC中点,∴△DCF≌CBE.△∠CDF=∠BCE又∠CDF+∠DFC=900BCE∴∠+∠DFC=900∴DFCE⊥又因为CC1⊥平ABCDC∴1E在平面ABCD内的射影为CE。由三垂线定理知C1EDF⊥小结•三垂线定理:⊥在平面内的一条直线、如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。练习和作业1、已知:O为正方体AC1的底面ABCD的中点。求证:D1OEF⊥2、已知P为△ABC所在平面外一点,若P在平面ABC内的射影是△ABC的垂心。求证:PABCPBACPCAB⊥⊥⊥3、如图,PO是平面α的斜线,O为斜足,PA⊥α于A,OC在平面α内ABDC于B若PO与平面α成300角,∠AOB=450。PA=2cm求:⑴PB的长⑵∠POB的大小ABCDA1B1C1D1OEFPOAαB再见