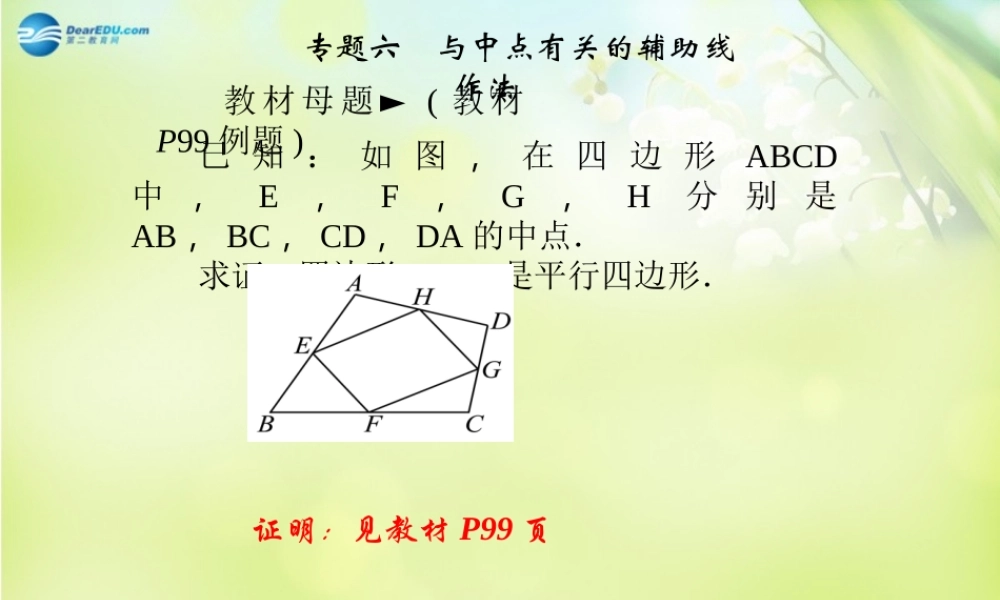
专题六 与中点有关的辅助线作法教 材 母 题 ► ( 教 材P99 例题 )已 知 : 如 图 , 在 四 边 形ABCD中 ,E,F,G,H分 别 是AB , BC , CD , DA 的中点.求证:四边形 EFGH 是平行四边形.证明:见教材 P99 页 【思想方法】 (1) 连接对角线,把四边形转化为三角形体现了转化思想.(2) 遇到中点找中点,这种方法常用于解决三角形和四边形的有关问题,主要是连接两个中点作中位线.因此,在三角形中,已知三角形两边中点,连接两个中点,即可构造三角形的中位线.(3) 遇到中点作中线,这种方法常用于解决直角三角形或等腰三角形的有关问题,主要是运用直角三角形斜边上的中线或等腰三角形底边上的中线的性质.因此,遇到直角三角形斜边上的中点或等腰三角形底边上的中点,应联想到作中线.变形 1 如图,在锐角三角形 ABC 中,分别以 AB , AC 为边向外作等边三角形ABM , ACN ,已知 D , E , F 分别是 BM ,BC , CN 的中点,连接 DE , EF. 求证: DE= EF.证 明 : 连 接 CM , BN , 先 证△AMC≌△ABN,得 MC=BN.由三角形中位线定理,得 DE=12MC,EF=12BN,于是可得 DE=EF. 变形 2 如图,DB,CE 分别是△ABC 的外角平分线,过点 A 作 AF⊥BD,垂足为 F,AG⊥CE,垂足为 G.求证:FG=12(AB+CB+AC). 证明:延长 AF 交直线 BC 于点M ,延长 AG 交直线 BC 于点N.∵BD 平分∠ ABM ,∴∠ ABF =∠ MBF.∵AF⊥BD ,∴∠ AFB=∠ MFB.∵BF =BF ,∴△ AFB≌△MFB.∴AF= MF , AB = BM. 同理可证AG = NG , AC = CN.∴FG 是△ AMN 的中位线.∴FG=12MN=12(MB+BC+CN)=12(AB+CB+AC). 变形 3如 图 , 在 四 边 形 ABCD 中 , AB =CD , M , N 分别是 BC , AD 的中点.求证:∠ BEM =∠ CFM.证明:如图,连接 AC ,取 AC 中点 G ,连接 NG , MG.∵M , N 分别是 BC , AD 的中点,∴ NG 是△ ACD 的中位线,MG 是△ABC 的中位线.∴NG∥CD 且 NG=12CD,MG∥AB 且 MG=12AB.∵AB=CD,∴NG=MG.∴∠1=∠2.∵NG∥CD,∴∠1=∠CFM.∵MG∥AB,∴∠2=∠BEM.∴∠BEM=∠CFM.