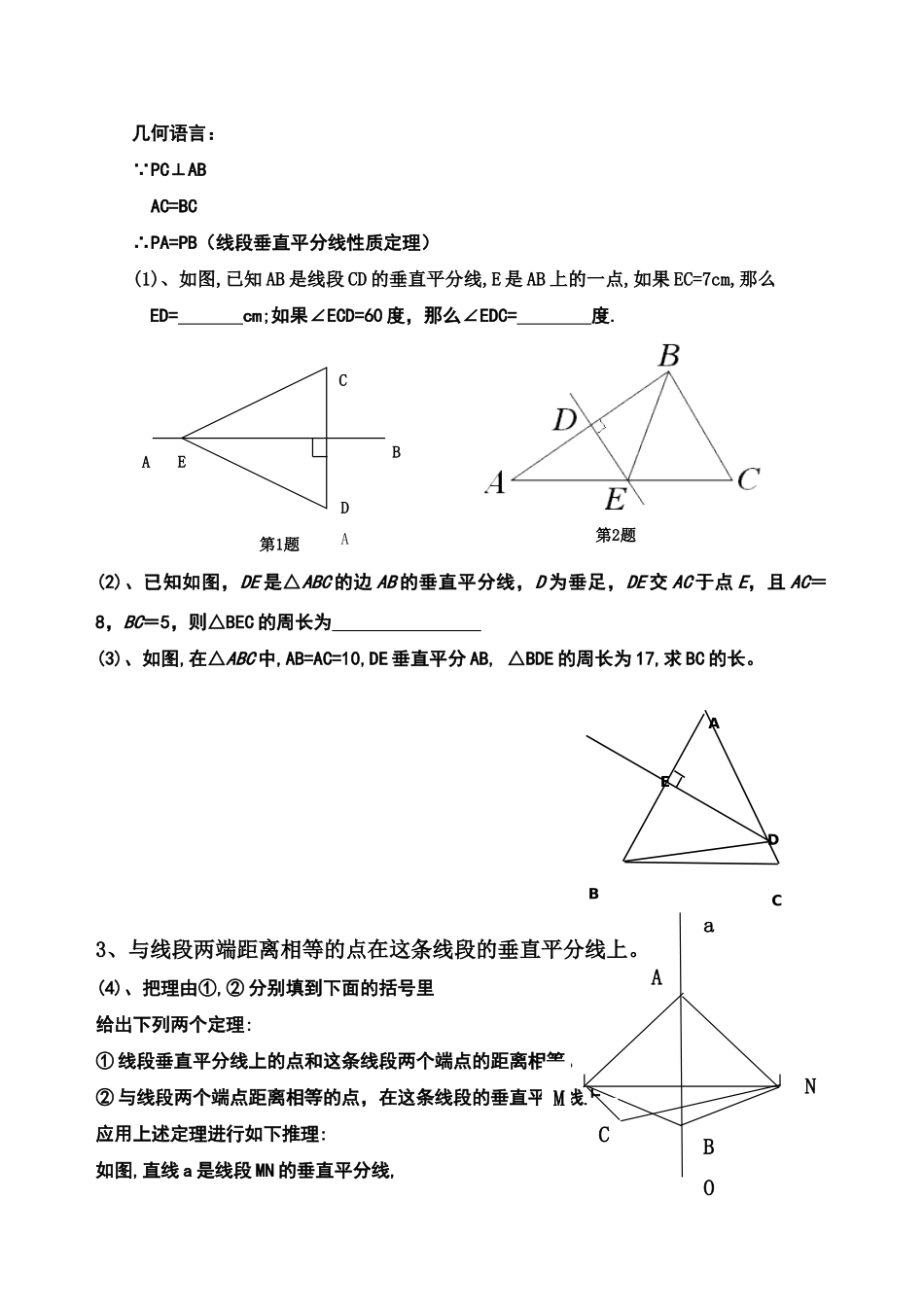
线段的垂直平分线目的要求:1.掌握线段垂直平分线的性质定理及判定定理;2.熟练地应用线段垂直平分线的性质及判定进行论证。重点、难点:重点:掌握线段的垂直平分线性质定理及判定定理;难点:认识垂直平分线性质定理及判定定理的关系。教学过程:一、复习1、什么叫线段的垂直平分线?2、用尺规作图:作线段AB的垂直平分线。二、新授1、导入新课通过作一条线段AB的垂直平分线入手,如图观察图形,发现图中的C、D点有何性质?2、线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。已知,如图,直线MN经过线段AB的中点O,且MN⊥AB,P是MN上任意一点。求证:PA=PB证明:∵MN⊥AB(已知)∴∠PCA=∠PCB(垂直定义)在△PCA和△PCB中:AC=CB(已知)∠PCA=∠PCB(已证)PC=PC(公共边)∴△PCA≌△PCB(SAS)∴PA=PB(全等三角形的对应边相等)ABABNMPO几何语言:∵PC⊥ABAC=BC∴PA=PB(线段垂直平分线性质定理)(1)、如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED=cm;如果∠ECD=60度,那么∠EDC=度.(2)、已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为(3)、如图,在△ABC中,AB=AC=10,DE垂直平分AB,△BDE的周长为17,求BC的长。3、与线段两端距离相等的点在这条线段的垂直平分线上。(4)、把理由①,②分别填到下面的括号里给出下列两个定理:①线段垂直平分线上的点和这条线段两个端点的距离相等。②与线段两个端点距离相等的点,在这条线段的垂直平分线上。应用上述定理进行如下推理:如图,直线a是线段MN的垂直平分线,ADCBEDABEAC第1题第2题MNABOCa∵点A在直线a上,∴AM=AN。()∵BM=BN∴点B在直线a上。()∵CM≠CN∴点C不在直线a上。因为如果C在直线a上,那么CM=CN.()这与条件CM≠CN矛盾(5)、已知:如图,△ABC中,AD是角平分线,DE⊥AB于E,DF⊥AC于F,求证:AD垂直平分EF.(6)、如图A、B是公路同侧两所中学,为解决学生坐公交车问题,公共汽车公司准备在笔直的公路两校之间设一个车站,(1)为使两校学生同时到达学校(或车站),车站最好设在何处?(2)为使两校学生走的路程的总长度最短,车站最好设在何处?(7)、已知,在△ABC中,AC<AB,∠A的平分线与BC的垂直平分线DM相交于点D,过D作DE⊥AB于E,DF⊥AC于F。ABCDEFmBAA求证:BE=CF小结:一个方法:证明线段相等的新方法:利用线段垂直平分线的性质。两条定理:线段垂直平分线上的点与线段两端的距离相等。与线段两端距离相等的点在这条线段的垂直平分线上。CBDEFM